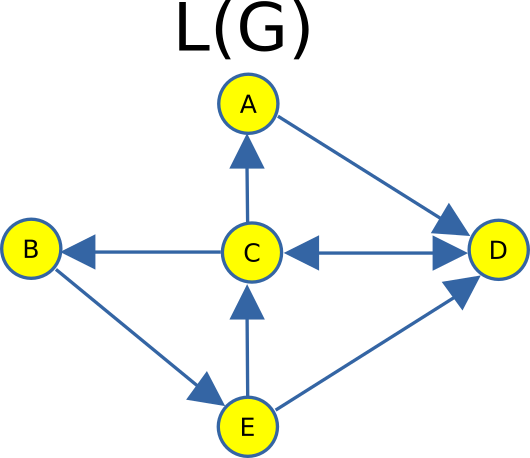
If G is a directed graph, any edges in L(G) that do not correspond to valid directional paths in G should be removed. Specifically, if no feasible path exists between two edges in G—even if they share a common vertex—they should not be connected in L(G).
For example, consider two edges, A and B, in G that are both directed outward from node 1. Although they share a common vertex, there is no possible way to traverse from A to B through node 1, nor in the reverse direction. Consequently, an edge between A and B should not exist in L(G).
Furthermore, the directionality of edges in L(G) must be consistent with the directional constraints of G. For instance, if a path exists from edge E to node 4, which subsequently leads to edge C, then L(G) should include a directed edge E → C. However, if starting from C allows traversal to node 4 but does not permit reaching edge E, then the reverse connection C → E should not be included in L(G). This ensures that L(G) faithfully preserves the directional flow of the original graph G.

Finally, we proceed to remove the original edges and nodes. As a result, the line graph will take the following form: